Imagina que o teu clube de futebol favorito ganha três jogos consecutivos por goleadas. A euforia é tanta que já se fala em campeonato. Mas, no jogo seguinte, o teu clube perde. E no outro, empata. O que aconteceu? A resposta está num fenómeno estatístico descoberto por Francis Galton no século XIX – a regressão à média (inicialmente chamou-lhe reversão). Este conceito, que parece simples, tem implicações profundas e muitas vezes contra-intuitivas. É o que explica porque é que desempenhos excepcionalmente bons tendem a ser seguidos por resultados mais “normais”. E, caso estejas a pensar na fase excepcionalmente atípica em que o F.C.Porto se encontra, o inverso também acontece!

Então, o que é a Regressão à Média?

A regressão à média é a tendência de eventos extremos — sejam eles excepcionalmente bons ou maus — serem seguidos por eventos mais próximos da média. Galton descobriu este fenómeno ao estudar a altura dos filhos em relação aos pais. Ele observou que pais muito altos tendiam a ter filhos altos, mas não tão altos quanto eles. O mesmo acontecia com pais muito baixos: os filhos eram baixos, mas não tão baixos quanto os pais.

Em termos estatísticos, a regressão à média ocorre porque os eventos extremos são muitas vezes o resultado de uma combinação de factores, alguns dos quais são aleatórios. Quando esses factores aleatórios não se repetem, o resultado tende a voltar ao valor médio.

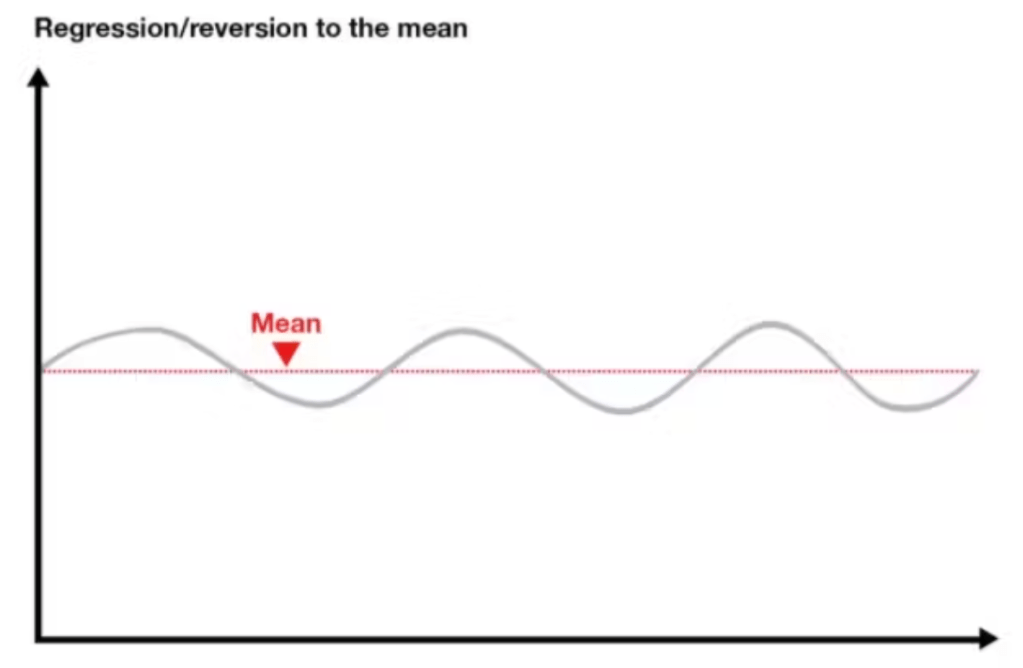
Compreender esta flutuação em torno da média (curvas) é essencial para analisar se o padrão médio (linha) se mantém constante ao longo do tempo ou se está a subir ou a descer. Assim, as observações pontuais devem ser criticamente analisadas em função da sua relação com a média.

A Matemática por Trás da Regressão

Para entender a regressão à média, podemos usar o conceito de correlação. (Também este conceito foi desenvolvido por Galton, assim como a psicometria ou a eugenia, mas deixo para outro texto mais história sobre este primo de Charles Darwin – Francis Galton e o desenvolvimento de testes de inteligência!)

Então, a correlação mede a associação linear entre duas variáveis, como a altura dos pais e a dos filhos. Se a correlação for perfeita (1), os filhos teriam exatamente a mesma altura que os pais. Se fosse zero, não haveria relação alguma. Suponhamos que queremos prever como um valor Y depende de um outro valor X. A equação de regressão é dada por:

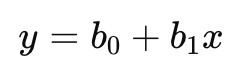
Aqui, b₀ (Beta zero) é o ponto onde a linha de regressão cruza o eixo Y, e b₁ (Beta um) mede quanto Y muda para cada unidade de X. Quando a correlação (r_xy) entre X e Y não é perfeita (ou seja, −1<r_xy<1), observamos a regressão à média. Em termos simples, a próxima medida de Y será, provavelmente, menos extrema do que X.

Vamos seguir o raciocínio de Galton em Natural Inheritance: uma criança alta, com pais mesmo muito altos, ainda será alta, mas provavelmente não tão alta como os pais. É como se a “altura” voltasse a aproximar-se do valor médio da população. Consideremos a correlação entre pais e filhos de cerca de 0,66. Isto significa que os filhos de pais muito altos (ou baixos) tendem a ser mais próximos da média da população, embora ainda reflitam, em parte, a altura dos pais. Consideremos esta fórmula para prever a altura dos filhos com base na dos pais:

Altura do Filho = Média da População + Correlação × (Altura do Pai − Média da População)

Se a altura média for 1,70 metros e o pai tiver 1,98 metros, a altura prevista do filho seria:

1,70 + 0,66 × (1,98 − 1,70) ≈ 1,88 metros

Ou seja, o filho, provavelmente, seria mais alto que a média da população, mas não tão alto quanto o pai.

A regressão à média tem implicações em muitas áreas, desde o desporto até a medicina. Por exemplo, se um jogador de futebol marcar três golos num jogo, é provável que no jogo seguinte marque menos. Isto não significa que ele tenha piorado, mas sim que o desempenho excepcional foi, em parte, resultado de factores aleatórios, como sorte ou defesas fracas.

O fenómeno da regressão para a média tem sido estudado em epidemiologia e descrito, desde Galton, em multiplas variáveis como o peso ao nascer, pressão arterial ou colesterol.

Armadilhas e Mal-Entendidos

Um erro comum é atribuir a regressão à média a causas específicas. O psicólogo Daniel Kahneman, vencedor do prémio Nobel, menciona na sua famosa obra Thinking Fast and Slow, o episódio que viveu na década de 60, quando lhe foi pedido pelo governo de Israel que ajudasse no treino de pilotos da força aérea. Notaram os oficiais responsáveis pelo treino dos pilotos que, após elogios, os cadetes faziam pior, mas após críticas, melhoravam. Isto levou os instrutores a concluir, erradamente, que criticar era melhor do que elogiar. Na verdade, era apenas a regressão à média em ação: após um desempenho extremo (bom ou mau), é natural que o próximo seja mais “normal”.

Veja-se ainda a falácia do jogador, a crença de que eventos aleatórios estão “em dívida”. Por exemplo, se uma moeda sair cara 10 vezes seguidas, algumas pessoas pensam que é mais provável que saia coroa na próxima jogada. Na realidade, a probabilidade continua a ser 50%, porque cada lançamento é independente. A moeda não tem memória do que aconteceu antes.

Assim, se alguma vez te sentires tentado a atribuir um resultado excepcional a uma causa específica, pensa que a regressão à média pode estar a trabalhar nos bastidores, trazendo os eventos de volta ao seu curso natural. Afinal, como diz o ditado, “o que sobe, desce” — e a matemática está lá para nos explicar porquê!

---

Esta descoberta, que começou com a altura dos filhos e dos pais, continua a influenciar a forma como entendemos o mundo à nossa volta. E, como vimos, por vezes, a verdadeira sabedoria está em aceitar que o extraordinário é frequentemente apenas uma flutuação temporária. Por isso, calma, se tens um amigo portista que está a sofrer, envia-lhe este texto, talvez ajude! O F.C.Porto em breve estará de regresso ao seu desempenho médio – vitorioso!