Abraham de Moivre e a Curva de Bell: A Descoberta da Distribuição Normal

Imagina que estás a jogar um jogo de dados. Lança dois (ou mais) dados centenas de vezes e anota a soma dos valores obtidos em cada lançamento. Se fizeres um gráfico com a frequência de cada soma, o que pensas que vai acontecer? Se estás a pensar num gráfico em forma de sino, estás no caminho certo! Essa curva elegante e simétrica é conhecida como curva de Bell ou distribuição normal, e é uma das ferramentas mais importantes da estatística. Mas quem foi o génio por trás desta descoberta? Apresento-te Abraham de Moivre, matemático francês que viveu no século XVIII, um dos meus heróis favoritos da estatística.

Quem foi Abraham de Moivre?

Abraham de Moivre era um huguenote (um protestante francês) que fugiu para Inglaterra após a revogação do Édito de Nantes, que protegia os protestantes em França. Em Inglaterra, ele tornou-se num matemático brilhante, conhecido por trabalhar com probabilidade e estatística. Ele era tão bom que consta que até o famoso Isaac Newton dizia: “Vão falar com o Sr. de Moivre; ele sabe estas coisas melhor do que eu.” Imagina só receber um elogio desses do próprio Newton!

A Descoberta da Curva de Bell

De Moivre estava a estudar jogos de azar, como lançamentos de dados, quando percebeu que os resultados tendiam a seguir um padrão. Esse padrão era a tal curva em forma de sino (Bell, em inglês). Ele descobriu que, quando se repetia um evento aleatório muitas vezes (como lançar um dado ou medir a altura de pessoas), os resultados agrupavam-se em torno de um valor médio, com menos resultados à medida que se afastavam desse valor. Por exemplo, se medires a altura de todos os adultos em Portugal, a maioria terá uma altura próxima da média (digamos, 1,70 metros), e poucos serão muito altos (2 metros) ou muito baixos (1,50 metros). Assim, se fizeres um gráfico com essas alturas, obterás uma curva em forma de sino (Bell).

De Moivre fez contribuições significativas para a teoria da probabilidade, incluindo a aproximação da distribuição binomial à distribuição normal, um resultado que antecipou o teorema do limite central. O seu livro The Doctrine of Chances foi pioneiro no campo, assim como a sua fórmula para estimar fatoriais, mais tarde refinada por James Stirling, que foi crucial para o desenvolvimento da análise combinatória. Além disso, de Moivre explorou a aplicação da probabilidade em problemas atuariais, publicando trabalhos sobre anuidades e taxas de mortalidade.

A Fórmula Mágica

A curva de Bell é descrita por uma fórmula que pode parecer assustadora à primeira vista, mas vamos simplificá-la:

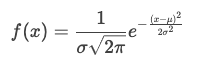
O que isto significa? Vamos por partes:

• μ (mu) é a média, ou seja, o valor central em torno do qual os dados se agrupam.
• σ (sigma) é o desvio padrão, que mede o quanto os dados se espalham em torno da média.
• e é o número de Euler, uma constante matemática (aproximadamente 2,718).
• π é o nosso velho amigo pi (3,1416…).

A fórmula pode parecer complicada, mas o que ela faz é simples: diz-nos a probabilidade de um valor x ocorrer, dado a média e o desvio padrão. Por exemplo, se a altura média for 1,70 metros e o desvio padrão for 10 cm, a fórmula permite-nos saber qual a probabilidade de alguém ter 1,80 metros ou mais.

Porque é que a Curva de Bell é tão Importante?

A distribuição normal é incrivelmente útil porque descreve muitos fenómenos naturais. Desde a altura das pessoas até aos erros de medição em laboratórios, passando pelos resultados de testes escolares, a curva de Bell aparece em todo o lado. Ela permite-nos fazer previsões e calcular probabilidades de forma precisa. Por exemplo, se soubermos que os resultados de um exame seguem uma distribuição normal, podemos prever quantos alunos vão ter notas altas ou baixas. Ou, se estivermos a fabricar parafusos, podemos usar a curva de Bell para garantir que a maioria deles tem o tamanho certo!

A Curva Bell ou A Curva de Gauss

Abraham de Moivre: O Pioneiro

Como já vimos, Abraham de Moivre foi o primeiro a descrever a curva de Bell no início do século XVIII. Ele estava a estudar probabilidade e jogos de azar quando percebeu que muitos fenómenos aleatórios seguiam um padrão em forma de sino. No entanto, o trabalho de de Moivre não teve o reconhecimento imediato que merecia, talvez porque ele era um huguenote exilado em Inglaterra e não fazia parte da elite científica da época.

Aliás, apesar das suas contribuições, de Moivre viveu pobre e morreu pobre, uma vez que nunca conseguiu uma posição académica estável, possivelmente devido ao preconceito contra as suas origens francesas. Morreu com 87 anos a 27 de novembro de 1754, em Londres, após prever a data da sua morte com base num cálculo matemático relacionado com o aumento do seu tempo de sono. Parece incrível, e não se sabe bem até que ponto se trata de um mito estatístico ou não, mas se quiseres saber mais sobre a capacidade preditiva da sua própria morte, explora aqui.

Carl Friedrich Gauss: O “Príncipe dos Matemáticos”

Entra em cena Carl Friedrich Gauss, um dos maiores matemáticos de todos os tempos. No início do século XIX, Gauss redescobriu a curva de Bell enquanto estudava erros de medição em astronomia. Ele percebeu que os erros nas medições tendiam a seguir uma distribuição em forma de sino, e desenvolveu métodos para lidar com esses erros. O trabalho de Gauss foi tão influente que a curva acabou por ser associada ao seu nome, especialmente na Europa continental.

Porque é que a Curva tem Dois Nomes?

Na realidade até tem mais. Aqui está a parte divertida: a curva de Bell e a curva de Gauss são a mesma coisa! A diferença está apenas no crédito histórico. Nos países de língua inglesa, é mais comum chamarem-lhe curva de Bell (Bell Curve), enquanto na Europa continental, especialmente na Alemanha, é mais conhecida como curva de Gauss (Gaussian Curve).

E Laplace? Ah, Sim, Laplace!

Para complicar um pouco mais, o matemático francês Pierre-Simon Laplace também contribuiu para o estudo da distribuição normal. Ele generalizou o trabalho de de Moivre e de Gauss, ao demostrar como a curva podia ser aplicada a uma variedade de fenómenos naturais. Por isso, em alguns contextos, também se fala da distribuição de Laplace-Gauss.

Conclusão: Quem Merece o Crédito?

A verdade é que todos eles merecem! De Moivre foi o pioneiro, Gauss popularizou a curva no contexto dos erros de medição, e Laplace expandiu o seu uso. Hoje, a distribuição normal é um conceito tão fundamental que é difícil atribuir o crédito a uma única pessoa.

Portanto, da próxima vez que ouvires falar da curva de Bell ou da curva de Gauss, lembra-te de que se está a falar da mesma coisa. E, se quiseres ser politicamente correto em estatística, podes sempre chamar-lhe distribuição normal — assim, ninguém fica de fora!